Vibration Measurement
Amplitude, frequency, phase, and mode shapes make it possible to quantify the dynamic behavior of a component. An overview of measured variables and analysis methods.
3 min readVibration Measurement & Signal Analysis
Vibration measurement enables the precise analysis of mechanical vibrations.
Vibration measurement is a key method in modern metrology that enables engineers to accurately record and analyze mechanical vibrations. It plays a crucial role in the monitoring, vibration analysis, and maintenance of machinery and structures across a wide range of industries.
Fundamentals of Vibration Measurement
Vibration measurement is the process of detecting and analyzing vibrations that occur in a mechanical system. These vibrations can be caused by a variety of factors, such as moving machine components, external forces, or structural instabilities. Vibration analysis enables engineers to determine vibration frequencies and amplitudes and draw conclusions about the condition and performance of the system.
How a vibration sensor works
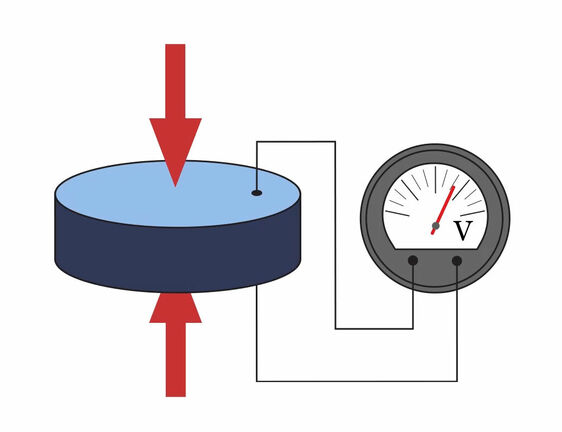
Vibrations are detected using vibration sensors such as piezoelectric accelerometers. These sensors convert mechanical motion into electrical signals. When the object being measured vibrates, the mechanical stress causes the sensor to generate electrical charges. These signals are amplified and analyzed to determine the object's motion characteristics. A typical vibration measurement instrument incorporates these sensors and provides a comprehensive platform for vibration measurement and analysis.
Why Is Vibration Measurement Important?
Vibration measurement makes it possible to identify potential problems early and take appropriate maintenance action. Regular vibration measurements can detect anomalies and signs of wear before they lead to major failures. This is particularly important in industrial manufacturing, aerospace, and construction, where the safety and reliability of machinery and structures are critical.
Vibration Measurement Methods
Vibration measurements are generally performed by mounting vibration sensors at critical points in the system. These sensors record mechanical vibrations and transmit the data for analysis. The fast Fourier transform (FFT) is a common method for analyzing this data, as it decomposes time-domain signals into their frequency components. This enables a detailed analysis of vibration frequencies and amplitudes.
Laser Doppler Vibrometer: An Advanced Measurement Instrument
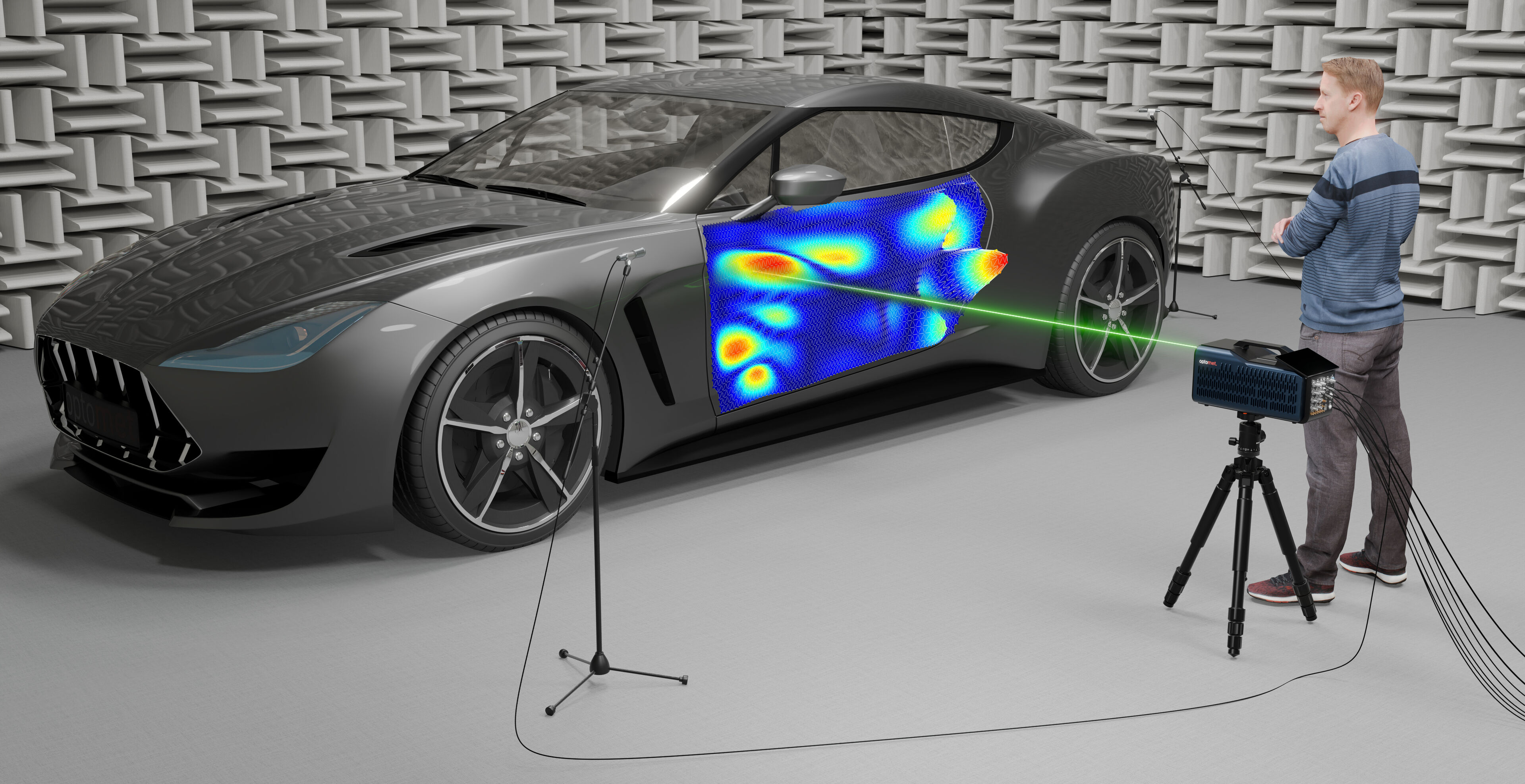
A laser Doppler vibrometer (LDV) provides a non-contact method for precise vibration measurement. Based on the Doppler effect a laser beam is focused on the surface to be measured. When the surface moves, the frequency of the reflected laser light changes. This frequency shift is evaluated using an interferometer. A photodetector then converts the optical signal into an electrical signal. Demodulating the signal provides precise information about the motion of the surface. This technology delivers the highest level of precision and is used in many demanding applications, such as aerospace and microstructure engineering.
An outstanding example of advanced vibration measurement equipment is the SMART Scan+. This compact system offers an optimal Signal Processing and high accuracy, making it ideal for detailed vibration analysis.
Applications of Vibration Measurement
Vibration measurements are used in many fields. In industry, they are used to monitor production processes and ensure their quality. In research and development, they help investigate material properties and develop new technologies. In the automotive industry, vibration measurements enable NVH (Noise, Vibration, Harshness) analysis and help improve ride comfort. Vibration measurements are also important in medicine, for example when examining medical devices and biological structures.
Future Prospects and Innovations
Vibration measurement continues to evolve, driven by technological innovation. Modern vibration measurement systems and laser Doppler vibrometers offer ever-greater precision and ease of use. The integration of intelligent software and advanced sensor technologies makes it possible to capture and analyze even complex vibration patterns in detail. These developments are setting new standards in vibration measurement technology and expanding its range of applications across various industries.